10082. Shortest even path
Undirected
unweighted graph is given. Find the shortest path between two vertices of even
length.
Input. The first line contains four integers:
number of vertices n, number of edges
m (n, m ≤ 105),
source s and destination d (1 ≤ s, d ≤ n). Each of the
next m lines contains two integers a and b describing an undirected edge (a, b).
Output. Print the shortest distance from s to d. The length of the path (number of edges in the path) must be
even. If there is no path of even length between s and d,
print -1.
|
Sample
input 1 |
Sample
output 1 |
|
8 8 1 6 1 2 2 3 3 4 4 5 5 6 4 7 7 8 8 6 |
6 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
6 5 1 6 1 2 2 3 3 4 4 5 5 6 |
-1 |
SOLUTION
graphs - bfs
Algorithm analysis
Split each vertex
v of the graph into two: v1
and v2. For each
undirected edge (u, v) create two undirected edges (u1,
v2) and (u2, v1).

For example, the
vertex v can be associated with vertices 2 * v – 1 and 2 * v.
The shortest
path between the vertices 2 * s – 1 and 2 * d – 1 will be the desired one and will have an even length.
Consider next
sample graph and splitted graph:
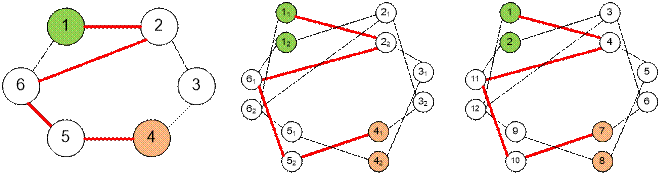
Let we start bfs
from the vertex v = 11. Then
·
if we’ll arrive to the vertex x1, the length of the path will be even;
·
if we’ll arrive to the vertex x2, the length of the path will be odd;
Finding the shortest path
of even length from 1 to 4 in the original
graph is equivalent to finding the shortest path from 11 to 41 (or from 1 to 7) in the
splitted graph.
Example
The graph in the
first example is shown on the left. The even shortest path is highlighted. In
the second example (picture on the right), there is no path of even length
between vertices 1 and 6.
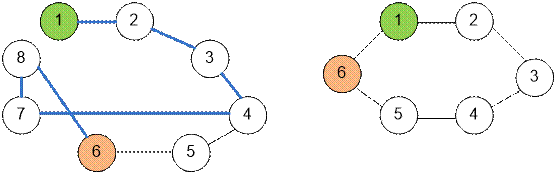
Algorithm realization
Declare an adjacency list g of
the graph and an array of shortest distances dist.
vector<vector<int>
> g;
vector<int>
dist;
Function bfs implements breadth first search from the vertex start.
void bfs(int start)
{
queue<int>
q;
q.push(start);
while
(!q.empty())
{
int v =
q.front(); q.pop();
for (int i =
0; i < g[v].size(); i++)
{
int to =
g[v][i];
if
(dist[to] == -1)
{
q.push(to);
dist[to] =
dist[v] + 1;
}
}
}
}
The main part of the program. Read the input data.
scanf("%d %d %d %d",
&n, &m, &s, &d);
g.resize(2*n + 1);
for (i = 0; i < m; i++)
{
scanf("%d
%d", &u, &v);
Read the edge (u, v). Split each of the vertices u and v into two. Create the edges (2*u, 2*v
– 1) and (2* v, 2*u – 1).
g[2*u].push_back(2*v-1);
g[2*v-1].push_back(2*u);
g[2*v].push_back(2*u-1);
g[2*u-1].push_back(2*v);
}
After splitting, the number of
vertices doubles.
n = 2 * n;
Initialize the array of shortest
distances.
dist = vector<int>(n
+ 1, -1);
dist[2*s-1] = 0;
Start the breadth first search from the start vertex.
bfs(2*s-1);
Print the answer.
printf("%d\n",
dist[2*d-1]);
Java realization
import java.util.*;
public class Main
{
static
ArrayList<Integer>[] g;
static int dist[];
static void bfs(int start)
{
Arrays.fill(dist,-1);
dist[start] =
0;
Queue<Integer> q = new
LinkedList<Integer>();
q.add(start);
while(!q.isEmpty())
{
int v = q.poll();
for(int i = 0;
i < g[v].size();
i++)
{
int to = g[v].get(i);
if (dist[to] ==
-1)
{
q.add(to);
dist[to] = dist[v] +
1;
}
}
}
}
@SuppressWarnings("unchecked")
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
int m = con.nextInt();
int s = con.nextInt();
int d = con.nextInt();
g = new
ArrayList[2*n+1];
for(int i = 0;
i <= 2*n; i++)
g[i] = new
ArrayList<Integer>();
for (int i = 0;
i < m; i++)
{
int u = con.nextInt();
int v = con.nextInt();
g[2*u].add(2*v-1);
g[2*v-1].add(2*u);
g[2*v].add(2*u-1);
g[2*u-1].add(2*v);
}
n = 2
* n;
dist = new int[n+1];
bfs(2*s-1);
System.out.println(dist[2*d-1]);
con.close();
}
}